“Compound interest is the eighth wonder of the world. He who understands it, earns it … he who doesn’t … pays it.” Albert Einstein

Has anyone wondered why the roads have become so congested so suddenly? Almost everywhere. Moscow, London, New York, Sydney. A dramatic increase in congestion and traffic in the past few years.

Here’s a little thought experiment derived by Professor Albert Bartlet of the University of Colorado about what might be happening. He uses bacteria and a bottle to show the dramatic effects of compounding rates of growth on a finite resource system – much like we have here on planet earth and on vehicles on the roads.

Bacteria grow by division so that 1 bacterium becomes 2, the 2 divide to give 4, the 4 divide to give 8, etc. Consider a hypothetical strain of bacteria for which this division time is 1 minute. The number of bacteria thus grows exponentially with a doubling time of 1 minute. One bacterium is put in a bottle at 11:00 a.m. and it is observed that the bottle is full of bacteria at 12:00 noon. Here is a simple example of exponential growth in a finite environment. This is mathematically identical to the case of the exponentially growing consumption of our finite resources of fossil fuels. Professor Albert Bartlet

So, when will the bottle be half full? At what time between 11 AM and 12 Noon?

Here’s the surprising answer:

At 11.59 am!

Here’s a table of the last 5 minutes in the bottle:

The last minutes in the bottle.
11:55 a.m.	1/32 full (3%)	31/32 empty
11:56 a.m.	1/16 full (6%)	15/16 empty
11:57 a.m.	1/8 full (12%)	7/8 empty
11:58 a.m.	1/4 full (25%)	3/4 empty
11:59 a.m.	1/2 full (50%)	1/2 empty
12:00 noon	full (100%)	0% empty

For most of the time in the bottle between 11 am and 12 Noon the bacteria consumed no more than 3% of available space. Then in the last 5 minutes, the bottle became full!

One of the special rules from compound exponential relationships is the “Rule of 7”: which says that a growth rate of 7% per year will double in 10 years. Conversely, when you take the growth of an expanding system and divide it into 7 and you’ll know the time it will take for the population of that system to double.

So let’s take the roads of Kuwait and her vehicles as an example: the cars are as the bacteria and the roads are as the bottle, the fixed resource.

In 2005 the number of vehicles in Kuwait was 1,134,000 and in 2013 the number was 1,743,000. That’s a yearly compounding increase of 5.5%.

Using the “Rule of 7”, therefore the doubling time is 12 years. Simply put, that means 1.743 million cars in 2013 will become 3,486,000 in 2025!

Can the Kuwait infrastructure handle it? Obviously not. The General Traffic Department of the Interior Ministry is adamant that the capacity of Kuwait Roads is only 800,000 vehicles. Already this number is exceeded by 120%.

Let’s go back to the example of the bacteria in the bottle.

Suppose that at 11:59am some smart bacteria realise that they only had one minute of available space left in their bottle. They decided to locate new bottles for their expanding population.

They found 3 more.

How long would these new bottles last?

Only 2 more minutes!

12:00 Noon – Bottle 1 is full.

12:01 PM – Bottle 2 is full.

12:02 PM – Bottles 3 and 4 are full.

So what should Kuwait do about vehicles? The roads are full and will only get more so. Should the road infrastructure be increased? If yes, then by how much? Double the present capacity? That simply won’t be enough as illustrated by the example with the bacteria in the bottle.

Applying the same to the population of Kuwait, the average population growth rate since 1997 is 4.5%. Using the Rule of 7, the doubling rate is 15 years. Presently 3.369m, by 2030, there will be 6.738 million people in Kuwait, if nothing changes. Therefore there will be 3.486 million cars.

With present capacity of the road system designed for 800,000 cars, that means a road system designed 4.5 times the capacity of the present system will be required in 2030. That’s a lot of road building. Also consider that by this will only satisfy the demand at that time with no further allowance for expansion. Which require a further 4.5 times capacity in another 15 years thereafter. Impractical? Yes. Something has to give. And that is natural resources – land, air quality, time.

Obviously allowing the number of vehicles to increase exponentially along with the population is not a viable solution for resource constrained Kuwait.

Other solutions will be put in place before then, and many of them must be implemented before their need is apparent, something we find difficult to do, planning ahead. It will take courage and foresight to do this.

This is the power of compounding growth. It highlights a fundamental problem with ever-expanding populations and production rates. When they occur in environments with finite resources (like ours) you see that it is only until the every last moments that it is apparent that anything needs to be done. By then it is too late. If prior adequate planning and investment has not been done, the systems will collapse. Things will break. The equilibrium will be out of balance. And this, as we have seen with the 30 year recession in Japan and the collapse of Greece, can take years to repair.

Let’s look briefly at two other exponentially growing systems that are undergoing regular, yearly expansion of only a few percentage points per year.

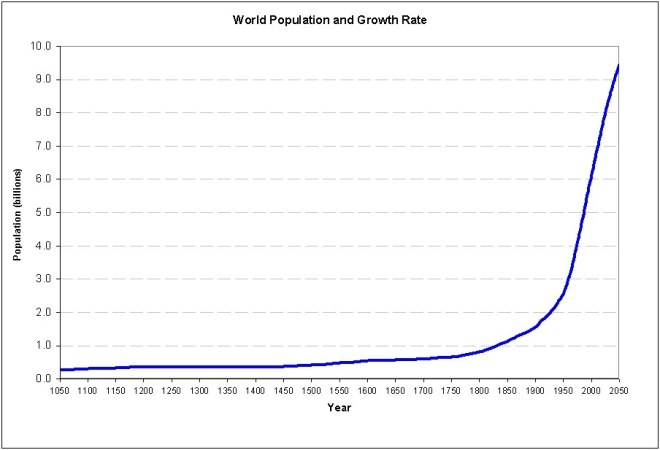
World Population: Presently 7.3 billion. Rate of growth: 1.14%. Doubling time 60 years.

The US M2 Money Supply. Presently 11.7 trillion. Annual growth 7%. Doubling rate: 10 years.

Both of these systems have not reached their natural resource limits. There is no correction apparent in their trends. Is that because of good planning or is the bottle simply not full yet.

I wonder what time it is?

Jeremiah